In continuum mechanics, the internal force is determined by the local deformation gradient and corresponding constitutive material model, while, in Peridynamics, it is replaced by an integral form with a set of non-local bond forces within a horizon. [Silling 2000] This makes Peridynamics very suitable in material failure analysis. The bond-based Peridynamics was implemented in LS-DYNA [1,2] using a framework of the discontinuous Galerkin FEM. FEM models can be used as input for Peridynamics analysis.
-
Advantage
-
Model crack initiation and propagation by breaking bonds
-
Capable to model complex failure modes
-
Mixed modes in 3D solid
-
In-plain failure, crossing lamina and delamination in laminate
-
-
-
Current implementation [kw][ex]
-
Bond-based Peridynamics
-
Discontinuous Galerkin FEM [1]
-
FEM model with detaching nodes as input
-
Bonds defined between integration (stress) points
-
-
Automatic conversion of material property [2]
-
From elastic modulus to bond micro modulus
-
From fracture energy release rate to bond critical stretching
-
-
3D solid & elastic material with brittle failure [kw]
-
Explicit analysis
-
-
Limitation
-
Elastic material with fixed Poisson's ratio (0.25)
-
-
Keyword
-
Application
-
Brittle material failure, e.g. windshield impact
-
Laminate failure, e.g. compression, drilling, jointing & impact
-
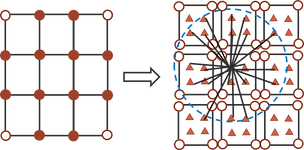
Discontinuous Galerkin: FEM model with detaching nodes
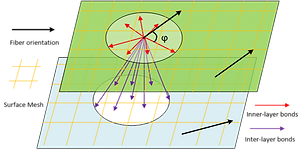
Inner-/inter-layer bonds with uniform mesh for laminate
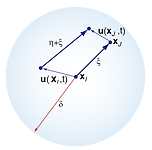
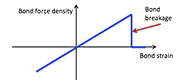
Non-local horizon & bond force

